Disease progression¶
Everyone suffers from a disease at some point. The lucky amongst us avoid anything more serious than influenza, measles, or (in my case, years ago) whooping cough. But all diseases share some common characteristics: characteristics so common, in fact, that their mathematical properties are shared by other processes that aren’t actually diseases at all, including the spread of computer viruses [10] and the spread of rumours and other information.
The diseases in which we are interested are caused by pathogens, typically viruses or bacteria: simple living organisms that make their homes in humans (or other living organisms) and cause some adverse reaction as a result of their lifecycle. These pathogens can pass between individuals in a number of ways, causing the disease to spread. A disease might be airborne, able to live in the air and be breathed by passing individuals. It might be spread by droplets, coughed and sneezed into the environment or deposited on objects and picked up by future physical contact with the contaminated surfaces. Or it might be communicable only by direct physical contact, skin to skin, through sex, or a blood transfusion. It might be foodborne, transmitted through contaminated food that infects several people from a common source. It might be vectored through an animal, as is the case for malaria which has to be sporead by mosquitoes and can’t spread person-to-person. Even diseases that don’t require a vector may still incubate in animal hosts as well as in humans (this is suspected in the case of the 1918 “Spanish flu” pandemic [16]). And finally there is a class of non-communicable diseases such as cancer or heart disease, some of which are hereditary: not caused directly by pathogens but perhaps influenced by their presence, and perhaps made worse by infections.
A disease becomes an epidemic when it infects a substantial fraction of a population within a short time. There’s no universally accepted definition of how large a fraction is needed to classify an outbreak as an epidemic: for new or rare diseases even a small number of infections might be considered an epidemic, while some diseases persist in a population at a low level and then flare-up epidemically. If an epidemic infects people in several populations – typically several countries or several continents – than it is termed a pandemic.
Each different kind of disease will have its own characteristic pathology, how it affects the body of a person infected. It will also have its own epidemiology that controls how it spreads. Clinically, both these characteristics are extremely important; we will focus here on the epidemiology, but the pathology remains important because factors involved in how a disease progresses in individuals may have a profound effect on how it spreads between individuals.
Disease progression¶
A person’s infection goes through several periods, starting with their disease progression;infection. Once infected, the disease resides latent in their system, developing its presence but not showing symptoms and not being infectious to others. After this latent period the disease becomes infectious, capable of being spread to others. Typically a person’s infectiousness peaks and dies away before the end of the disease progression.
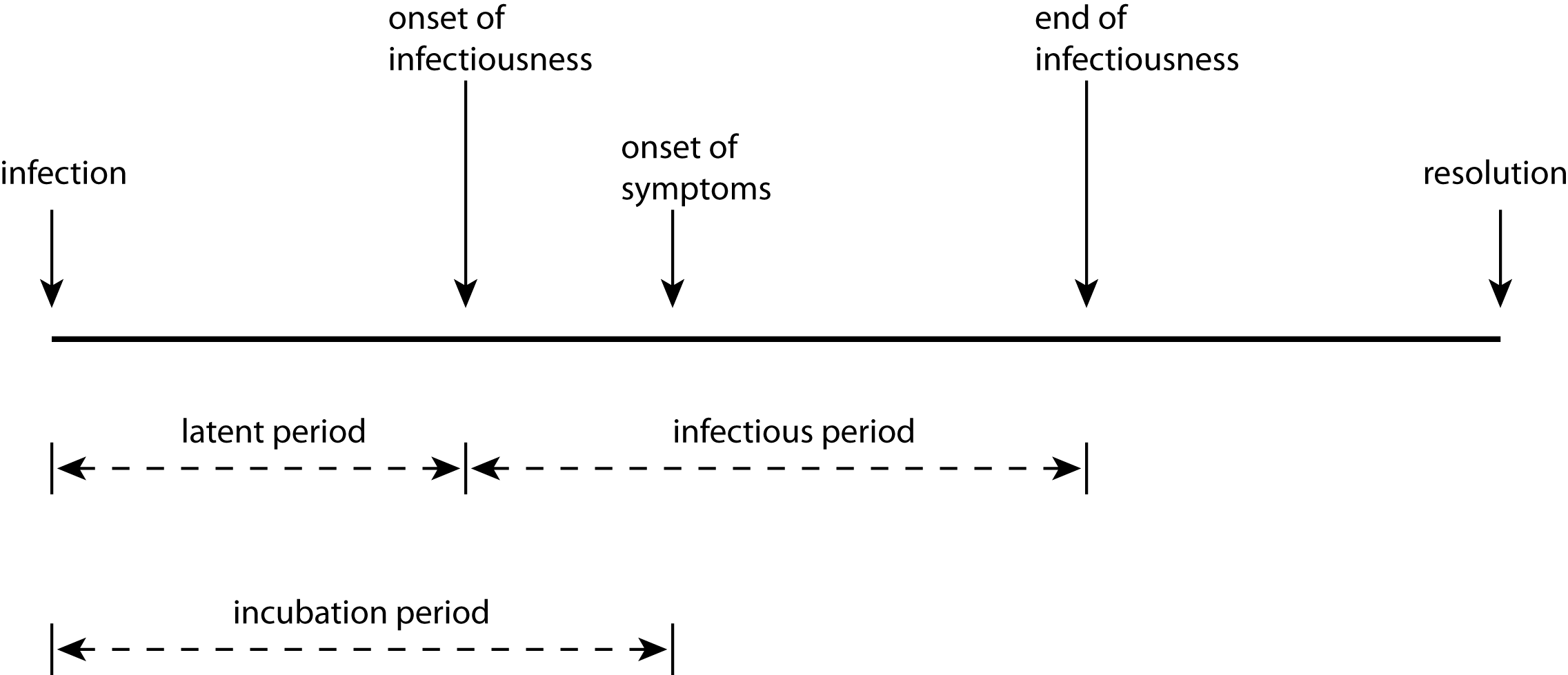
These two periods – latent and infectious – control the transamission of infection. After initial infection there will be an disease progression;incubation period before the person shows symptoms of the disease. After the onset of symptoms, the disease progresses and ends in some disease progression;resolution: the patient gets better, or dies. If they recover, they may then have some immunity to further infection.
For different diseases, the lengths of these periods and the ways they overlap vary. For Type A diseases, the incubation period is longer than the latent period. This means that a patient can start to transmit the disease before the disease becomes manifest in themselves. This happens in cases of measles and covid-19. In Type B diseases such as SARS or ebola, by contrast, the incubation period is shorter than the latent period, meaning that asymptomatic patients cannot infect others. So despite ebola being a more feared disease than measles, it may be easier to treat epidemiologically since quarantining patients showing symptoms will prevent transmission in the general population (although not to medical staff); in measles, transmission starts before symptoms show themselves, so quarantine based on symptoms is less effective. Moreover for some disease the infectious period may continue after the patient has died: the corpses of victims of ebola, which is transmitted via bodily fluids, can be extremely infectious for some time after death, meaning that funerals become very dangerous loci of potential infection for mourners.
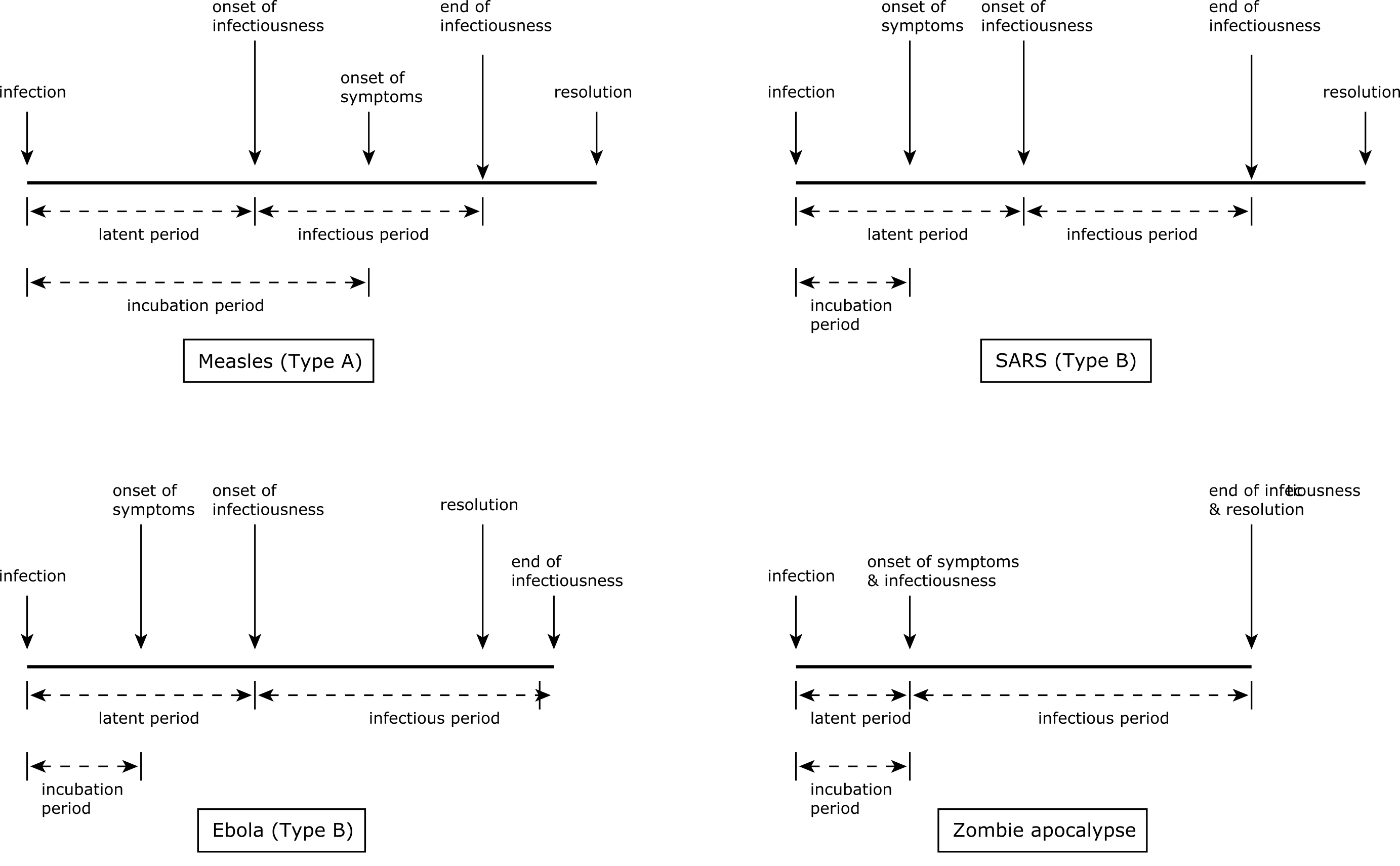
How long do the different periods last? For each disease there will be typical durations, often with substantial variance. In the case of ebola, for example, a typical timeline would be a 0–3 day incubation period, a 7–12 day progression to recovery or death, and a latent period of 2–5 days. The ranges give the variance of periods, different for different individuals that depend on factors including the severity of infection and the individual’s overall health. However, the incubation period for ebola can be up to 21 days, meaning that a suspected case needs to be quarantined for this period: long enough, in other words, for the disease symptoms to manifest if the person is actually infected. While one can test for most diseases (including ebola) in a laboratory, during an epidemic such tests may overwhelm the public health infrastructure, making quarantine the most practical option. (During historical disease outbreaks, of course, quarantine was the only option.)
Measuring and modelling epidemics¶
Epidemiology is the science of creating models of diseases and their spread that can be analysed, to make predictions or to simulate the effects of different responses. To do this, we need to identify the core elements of a disease from the perspective of transmission: we typically do not need to understand the disease’s detailed biology, only the timings and other factors that affect its spread.
We discussed above the periods of diseases, their relationships, and their different characteristics. We need some other numbers as well, however, and it turns out that these can be measured directly in the field.
The most important number is the basic case reproduction number, denoted \(\mathcal{R}_0\). \(\mathcal{R}_0\) represents the total number of secondary infections expected for each primary infection in a totally susceptible population. The \(0\) in \(\mathcal{R}_0\) stands for \(t = 0\): the basic case reproduction number applies at the start of an epidemic. Over the course of an epidemic the value of \(\mathcal{R}\) will change as people become immune post-infection, countermeasures take effect, and so forth, and give rise to a net case reproduction number indicating how the disease is reproducing at a given time.
\(\mathcal{R}\) is affected by three factors:
The duration of infectiousness. All other things being equal, a disease with a longer period of infectiousness has more time in which to infect other patients.
The probability of transmission at each contact. Some diseases are extremely contagious, with each contact having a high probability of passing on the infection; others are much harder to pass on to secondary cases.
The rate of contact. Someone coming into contact with more susceptible individuals will have more opportunities to generate a secondary case than someone meeting fewer. s
The first two factors are characteristic of the disease, derived from its biology. The third is characteristic of the social conditions in which the epidemic takes place: it is this factor that physical distancing, quarantine and so forth affect, by reducing (ideally to zero) the contacts an infected person has with uninfected individuals.
The importance of \(\mathcal{R}\)¶
The importance of \(\mathcal{R}\) is that it indicates whether, and how fast, a disease can spread through a susceptible population. If \(\mathcal{R} < 1\) then we expect fewer than one secondary case per primary. This means that each “generation” of the disease will be smaller than the one that infected it, and the disease will die out. If \(\mathcal{R} = 1\) then the disease will perpetuate itself in whatever size of population was originally infected. Nature is never so precise as to present us with a disease like this, of course. However, \(\mathcal{R} = 1\) is the threshold value at which diseases become epidemics. If \(\mathcal{R} > 1\), the disease will break-out and infect more and more people.
Exactly how quickly depends on how large \(\mathcal{R}\) is. For measles, \(\mathcal{R} \ge 15\) – fifteen new infections for each case – which explains how measles spread so quickly in unvaccinated populations. Different strains of influenza have different ranges of \(R\): for the 1918 “Spanish flu” it has been estimated [25] that \(1.2 \le \mathcal{R} \le 3.0\) in the community (although substantially more in confined settings). If this sounds benign, remember that this epidemic killed substantially more people than did the First World War.
In a typical epidemic the number of people infected grows very quickly. If \(\mathcal{R} = 2\) then one person infects two others, who each infect two others, who each … and so on – so each generation is twice as big as the last). If you plot the size of the epidemic against time on a graph, it’ll draw out an exponential curve.
Why we need to be careful about \(\mathcal{R}\)¶
This sounds like good news: if we know \(\mathcal{R}\), we can estimate the size of the epidemic we’re facing; if we calculate it on an on-going basis we can monitor how well any countermeasures we deploy are working, and decide when to relax those countermeasures.
Well, not quite. There are at least four reasons that mean we need to be careful not to over-rely on \(\mathcal{R}\).
The first reason is mathematical. \(\mathcal{R}\) is the exponent of the equation that controls the epidemic’s size. This is important, because it means that epidemics behave non-linearly. An \(\mathcal{R}\) value of 4 is not twice as bad as an \(\mathcal{R}\) value of 2: the epidemic isn’t twice as big, it doubles twice as many times in the same period. Small differences in the value of \(\mathcal{R}\) therefore have huge effects.
It’s true that \(\mathcal{R} = 1\) is the critical value, below which an epidemic dies out. But it doesn’t follow from this that an \(\mathcal{R}\) value slightly over 1 is “pretty much 1” and so not a worry. That non-linearity means that even a small excess in \(\mathcal{R}\) can lead to a large outbreak. This has implications for epidemic control too: reducing the \(\mathcal{R}\) value to just below 1 isn’t an indication that everything will then be fine, as a small increase may set things off again.
The second reason concerns estimation. The most effective way of estimating \(\mathcal{R}\) is contact tracing, where infected individuals’ contacts are located and tested – and can then be treated or isolated if found to be infected themselves. Careful and widespread “test, trace, and isolate” strategies can be extremely effective in reducing an epidemic. The number of infected contacts individuals have on average lets us estimate of \(\mathcal{R}\).
But by definition test and trace is “counting in the rear view mirror”. It tells us how many people were being infected, not how many people are being infected. There will be a delay in identifying infected individuals, further delay in finding and testing their contacts, and so forth. If circumstances are changing, for example through pathogen evolution or it infecting different social settings, the estimate will be rendered out of date.
The third reason concerns the consequences of errors. Finding, tracing, and counting of infected individuals is invariably error-prone. People will be missed; tests are never 100% accurate, especially for diseases with long incubation periods where there may be low pathogen loads in the early stages; individuals forget whom they were in contact with; tracing apps don’t work in all circumstances; and so forth. Each of these errors leads to under-counting secondary infections and therefore under-estimating \(\mathcal{R}\).
Finally we must remember that \(\mathcal{R}\) is the average number of secondary cases per primary. The use of averaging (and indeed other summary statistics) is essential when trying to get the “big picture” of an epidemic. But it means that the value of \(\mathcal{R}\) reported depends not just on the disease but on the population being averaged over.
To see what this might mean, consider a country consisting of one city surrounded by a collection of small villages – London in the Middle Ages might be a good example. Suppose the disease breaks out ferociously in the city but, because they are separated and take precautions, the villages see a much sparser rate of infection. If we were to compute the net case reproduction rate averaged over the city we’d capture all the ferocity of the epidemic’s spread. But if we compute the rate over the whole country, we’d see a far milder epidemic. Because the same disease is spreading in different circumstances, averaging may be misleading – too mild for the city, but too large for the countryside. When interpreting an average, you always need to know what population has been averaged over. It is possible to manipulate the reported \(\mathcal{R}\) value accidentally, or deliberately by judicious choice of population.
For all these reasons it’s important not to fixate on \(\mathcal{R}\). The fact that it’s a number can sometimes give a false sense of security, because numbers suggest certainty and precision – and measuring \(\mathcal{R}\) in the midst of an on-going epidemic offers neither. A value of \(\mathcal{R}\) that’s reducing over time is a good sign. But \(\mathcal{R}\) falling – or seeming to fall – below 1 isn’t enough to prove that countermeasures are working and can be relaxed.
Growth rates¶
You may have noticed that the definition of \(\mathcal{R}\) doesn’t include time. It’s essentially the ratio of the different sizes of two “generations” of infection, and so tells us about the way the disease reproduces itself in a population. But it doesn’t tell us how fast that reproduction happens: how long does it take for the “next generation” to come along?
Obviously the answer is something to do with the latent period we looked at earlier. The shorter the latent period, the faster an infected person becomes infectious, and the faster the epidemic will grow. \(\mathcal{R}\) tells us nothing useful about this rate of growth.
Clearly this rate matters for tackling an outbreak, as well as for modelling the progress of a disease in time. For this reason it’s common to use another, complementary measure of epidemic behaviour.
When we talked about the exponential growth in epidemic size, we were still thinking in terms of generations of disease. We can think in “real” time instead.
Mathematically, the size of an epidemic can be expressed as
where \(N(t)\) is the number of cases at time \(t\) (measured in some units) and \(\lambda\) is the growth rate, the number of new cases that appear per unit of time. The utility of this is that if we know the growth rate per day and we know how many disease cases we have now, we can predict how many diseases cases we’ll have later, tomorrow (or even farther into the future) – and more importantly we’ll know the answer in terms of days, not in terms of disease generations. Even more importantly, we can get \(\lambda\) directly from time series such as the number of diagnoses cases by fitting a theoretical curve to the collected data.
Just as \(\mathcal{R}\) had a threshold at \(\mathcal{R} = 1\) that determined whether the epidemic was growing or shrinking, so \(\lambda = 0\) divides growing (\(\lambda > 1\)) from shrinking (\(\lambda < 0\)) conditions. And just like \(\mathcal{R}\), we need to be careful about reading too much into that: mistakes or omissions in reporting the ongoing cases can easily cause an over- or under-estimate of \(\lambda\).
The values of \(\mathcal{R}\) and \(\lambda\) are mathematically related, of course, with the former being found by integrating the latter [26]. In fact we can make \(\lambda\) capture just the biological part of the disease’s spread, while capturing things like social issues and countermeasures separately as a probability distribution of infections over time.
Questions for discussion¶
Think of a disease you’ve had. How did you catch it? Could you have done anything to avoid catching it? Was it made worse by where you lived at the time?
What can be done to cope with “Type A” diseases, where people can transmit the disease without showing symptoms of it?
Do you think the \(\mathcal{R}\) number is a useful thing to keep track of during an epidemic? Why? (Or why not?)