Our paper “Percolation on random graphs with higher-order clustering” was accepted into Physical Review E.

This paper has been around quite a lot of reviewing cycles to get it right, and they’ve made it enormously stronger than when we first submitted it five months ago.

The paper looks at how clustering of a network affects the formation of a giant component when conducting percolation — which is something that also has huge importance in disease modelling, as percolation is closely relate mathematically to how diseases spread. The main result is that clustering — where there are triangles, squares and other cycles, as well as cliques and similar structures that “densify” the network locally — have an effect on the threshold at which percolation happens or at which disease break out.

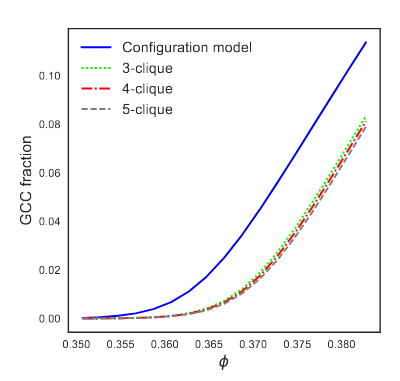
This is the basic work behind our recently-accepted applications paper, which uses a slightly extended theory to look at the ways in which these properties interact with other features commonly found in real-world networks.

It’s been a great few months for this work, and all credit belongs to Peter, my PhD student and the main author on both papers, for hanging-in when it seemed we might not make it into the venue we targeted.