We just put pre-prints of two new papers dealing with the analysis of clustered networks onto arXiv.

Its well-known that the topology of a network affects the way processes work over it: diseases spread more quickly when they occur in social networks that contain “hubs” with lots of social connections, for example. For a long time network science only considered the degree distribution of nodes - the number of contacts an individual has. But it turns out that the ways in which those contacts occur matter too.

In particular, human contact networks exhibit a feature called clustering. The easiest way to understand this is that the, if you have two friends, they are more likely to be friends themselves than are two randomly-chosen individuals: lots of people have mutual friends. This happens at longer distances as well, when you consider two of your friends also having another mutual friend — but one who isn’t a friend of yours.

Since infections often propagate through contacts, these structures change the way diseases move through a population. Specifically, they increase the probability of someone becoming infected, meaning that epidemics spread faster and become larger than you’d expect in systems that don’t have clustering.

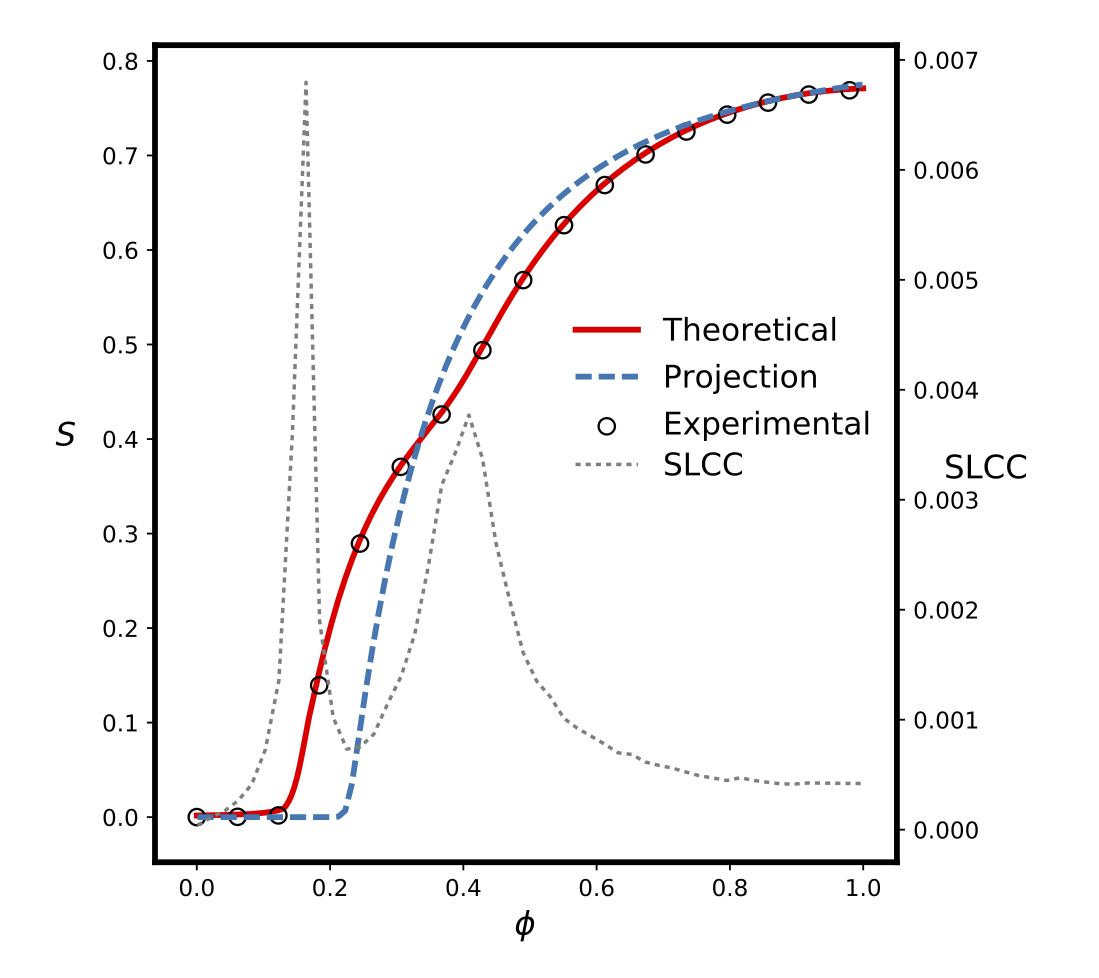
These two papers — mainly written by Peter Mann, and co-authored by Anne Smith, John Mitchell, and myself — look at the underlying mathematics of these clustered networks. We study both “weak” and “strong” clusters consisting of cycles of arbitrary length that may also have short-cuts across them. We derive a model that lets us predict the behaviour of percolation-type processes on these networks. There are some interesting phenomena on show, not least a suggestion us using the size of the second-largest component as a marker for phase changes in the largest (giant) component. We also look at how these results affect multiplex networks, of the kind one finds when two recognisably-distinct groups of people meet and mingle.

Both papers are under review by Physical Review E.